Уравнение касательной онлайн
Немного теории:
Что такое касательная?
Касательная к графику функции f, дифференцируемой в точке xо, — это прямая, проходящая через точку (xо; f(xо)) и имеющая угловой коэффициент f ′(xо).
Условие существования касательной к графику функции, проходящей через данную точку: Функция должна быть дифференцируема в этой точке
Угловой коэффициент равен тангенсу острого угла, образуемого этой прямой с осью абсцисс: k = tg α Что можно сказать о расположении касательных по отношению к оси абсцисс? (рис.1 и 2). 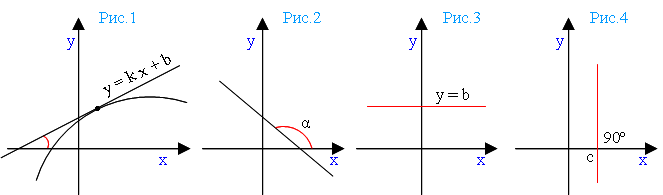 A) Если угол наклона прямой y = kx + b острый, то угловой коэффициент является положительным числом. График возрастает (рис.1). Б) Если угол наклона прямой y = kx + b тупой, то угловой коэффициент является отрицательным числом. График убывает (рис.2). В) Если прямая параллельна оси абсцисс, то угол наклона прямой равен нулю. В этом случае угловой коэффициент прямой тоже равен нулю (так как тангенс нуля есть ноль). Уравнение прямой будет иметь вид y = b (рис.3). Г) Если угол наклона прямой равен 90º (π/2), то есть она перпендикулярна оси абсцисс, то прямая задается равенством x = c, где c – некоторое действительное число (рис.4). Уравнение касательной к графику функции y = f(x) в точке xо:
A) Если угол наклона прямой y = kx + b острый, то угловой коэффициент является положительным числом. График возрастает (рис.1). Б) Если угол наклона прямой y = kx + b тупой, то угловой коэффициент является отрицательным числом. График убывает (рис.2). В) Если прямая параллельна оси абсцисс, то угол наклона прямой равен нулю. В этом случае угловой коэффициент прямой тоже равен нулю (так как тангенс нуля есть ноль). Уравнение прямой будет иметь вид y = b (рис.3). Г) Если угол наклона прямой равен 90º (π/2), то есть она перпендикулярна оси абсцисс, то прямая задается равенством x = c, где c – некоторое действительное число (рис.4). Уравнение касательной к графику функции y = f(x) в точке xо:
y = f(xо) + f ′(xо) (x – xо)
Алгоритм составления уравнения касательной к графику функции y = f(x):
| 1. Вычислить f(xо). 2. Вычислить производные f ′(x) и f ′(xо). 3. Внести найденные числа xо, f(xо), f ′(xо) в уравнение касательной и упростить его. |
Пример решения задачи на нахождение касательной:
Напишите уравнения всех касательных к графику функции y = – x2 – 4x + 2, проходящих через точку M(– 3; 6).
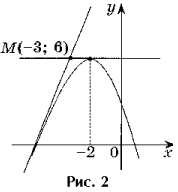
Решение.
Точка M(– 3; 6) не является точкой касания, так как f(– 3) 6 (рис. 2). 1. a – абсцисса точки касания. 2. f(a) = – a2 – 4a + 2. 3. f ‘(x) = – 2x – 4, f ‘(a) = – 2a – 4. 4. y = – a2 – 4a + 2 – 2(a + 2)(x – a) – уравнение касательной. Касательная проходит через точку M(– 3; 6), следовательно, ее координаты удовлетворяют уравнению касательной. 6 = – a2 – 4a + 2 – 2(a + 2)(– 3 – a), a2 + 6a + 8 = 0 a1 = – 4, a2 = – 2. Если a = – 4, то уравнение касательной имеет вид y = 4x + 18. Если a = – 2, то уравнение касательной имеет вид y = 6. В правительстве Украины вновь перемены. Первый зам министра, правая рука премьера уходит в отставку. Больше и подробнее о ситуации на Украине и не только

