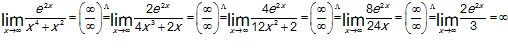Вычисление пределов функций с помощью правила Лопиталя
Неопределенности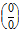 
и 
.
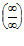Правило Лопиталя: Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных, если последний предел существует.
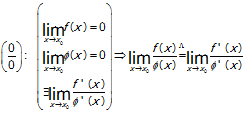
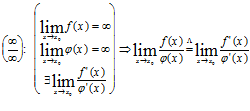
Буква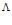 
над знаком равенства означает, что для вычисления предела применяется правило Лопиталя. В этих формулах х может стремиться и к бесконечности 
. Если после применения правила Лопиталя непределенность 
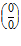или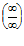 
сохраняется , то следует применить еще раз правило Лопиталя.
С помощью правила Лопиталя найти пределы.
1) 
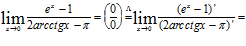
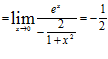
2) 
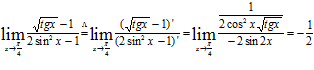
3) 
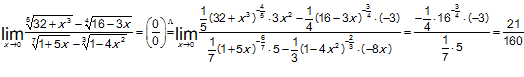
4) Здесь лучше в знаменателе (в числителе нельзя!) использовать эквивалентность бесконечно малых, а затем применить правило Лопиталя.
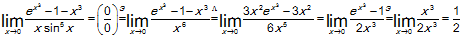
Буква Э над знаком равенства означает применение эквивалентности бесконечно малых.
В последнем примере показано как разумно сочетать эквивалентность бесконечно малых и правило Лопиталя.
5) 
