Свойства и вычисление определенного интеграла

Свойства определенного интеграла основываются на основной формуле интегрального исчисления.

1. Постоянный множитель можно вынести за знак определенного интеграла:

.

2. Определенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов от слагаемых:

.

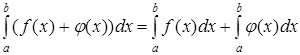3. В случае, когда a=b положим по определению, что

.

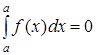4. В случае, когда b и a меняем местами

.

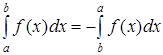5. От обозначения переменной значение интеграла не зависит:

.

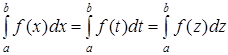6. Для любых трех чисел a, b и с справедливо равенство:

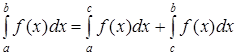
7. Если на [a, b] функции f(x) и φ(x) удовлетворяет неравенству 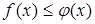, для всех 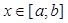, то .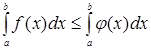

8. Определенный интеграл имеет знак подынтегральной функции на отрезке [a, b].

9. Свойство о среднем значение функции. Если f(x) непрерывна на [a, b], то внутри этого отрезка существует одна точка ξ, такая, что справедливо равенство:

.

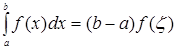Геометрически данное свойство утверждает, что на [a, b] существует такая точка ξ, что площадь криволинейной трапеции будет равновелика площади прямоугольника с тем же основанием и высотой.

10. Свойство Барроу. Производная от интеграла по верхнему пределу равна подынтегральной функции от верхнего предела, то есть:

.

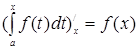11.Свойство модуля:

.

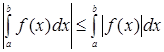Вычисление определенного интеграла

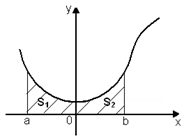
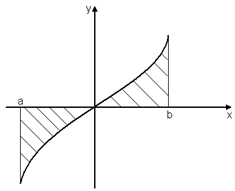
1. Рассмотрим определенный интеграл от четной и нечетной функций.

Пусть 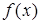четная: ,.

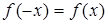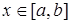Тогда:

.

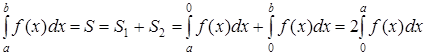Пусть 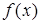– нечетная, то есть 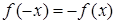, 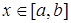. Тогда:

.

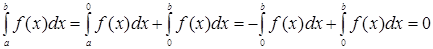2. Интегрирование по частям в определенном интеграле. Пусть даны две функции u(x), v(x), дифференцируемые для всех 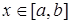. Тогда используя правила дифференцирования, можем утверждать:

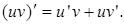
Интегрируем обе части равенства:

.

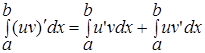
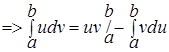Это формула интегрирования по частям в определенном интеграле.

3. Замена переменной в определенном интеграле. Пусть дан интеграл от непрерывной функции на [a, b]. Введем новую переменную x=φ(t), причем будем считать, что функция x=φ(t) непрерывна на [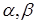], 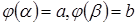. По формуле Ньютона-Лейбница имеем:

,

.

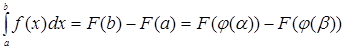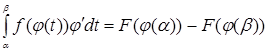Тогда имеем:

.

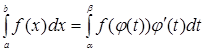Часто девушки, в том числе и студентки задаются вопросом? все ответы найдутся на сайте, посвященном красоте и здоровью, множество народных средств, которые обязательно Вам помогут!!!