Лекция №4. Бесконечно малые величины

Опр. 1: Переменная 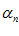называется бесконечно малой, если её пределом является нуль.

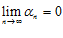
Определение на языке 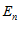: Переменная 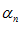называется бесконечно малой, если для любого E > 0 существует такой номер N, что при выполнении неравенства n > N, следует выполнение неравенства:

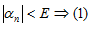
ПРИМЕРЫ:

1.    

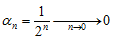
2.    

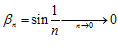
3. 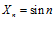       – не имеет предела.

ЛЕММЫ О БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИНАХ.

 ЛЕММА №1: Для того чтобы переменная 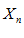имела своим пределом постоянное число a, необходимо и достаточно выполнения равенства:

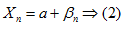
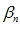    – бесконечно малая величина.

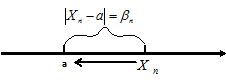
 Результат следует из того, что разность 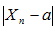есть расстояние от точки 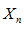до её предела 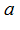, это расстояние стремится к нулю, т. к. 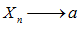, и наоборот: если расстояние стремиться к нулю, то .

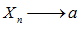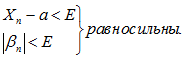
ЛЕММА №2: Алгебраическая сумма конечного числа бесконечно малых, есть величина бесконечно малая.

Доказательство:

Рассмотрим, например, сумму 3-х бесконечно малых.

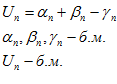
Возьмем любое E > 0, т. к. 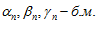,то по определению существует номер n такой, что будет выполняться три неравенства:

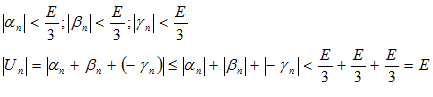(по лемме №2 о вещественных числах).

Существует номер n, такой, что при n > N выполняется неравенство:

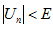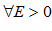    для , это и означает, что 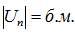, Ч. Т. Д.

Опр. 2: Переменная 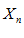называется ограниченной, если существуют такие m и M , что для всех 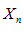выполняется неравенство: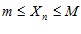

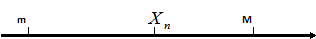
ПРИМЕР:

1. sin(n)  – ограниченное, т. к. |sin n| ≤ 1

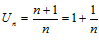
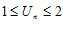
3. 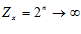       – не является ограниченным.

 (О. П. – ограниченная переменная).

 ЛЕММА №3:Произведение ограниченной переменной на бесконечно малую есть величина басконечно малая 

Пусть

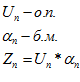
Требуется доказать, что: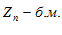  

Доказательство:

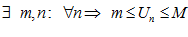
Пусть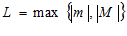

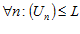
Возьмем 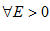, т.к. 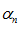– бесконечно малая, то существует номер N такой что при: ,

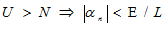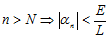
Тогда .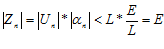

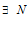     , при 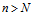, следовательно, выполняется неравенства:

    ,    

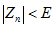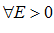
Это и означает, что: 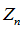– бесконечно малая.

Объявление: