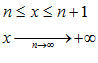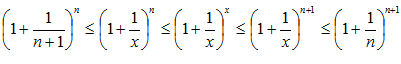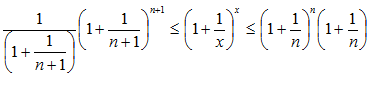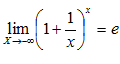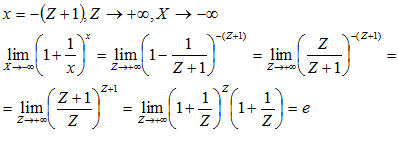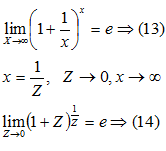Лекция №8. Замечательные пределы
Первый замечательный предел
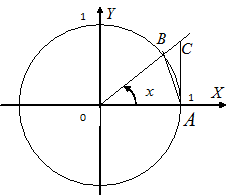
Функция Рассмотрим площади трех фигур:
Т. к. фигуры вложены друг в друга, то их площади связаны неравенством: Из неравенства (2) вытекает, что при Примеры решения пределов с помощью первого замечательного предела:
Второй замечательный предел.Переменная Переменная Переменная Переменная Все перечисленные переменные ТЕОРЕМА: Если переменная
Можно доказать, что переменная В дальнейшем будет выведена формула, позволяющая вычислить этот предел с любой степенью точности
Число С числом
Гиперболические функции:1. 2. 3. 4.
Свойства гиперболических функций функций:
Формулы гиперболической тригонометрии.
Для гиперболической функции существует система формул, составляющих так называемую гиперболическую тригонометрию. Основное гиперболическое тождество:
Доказательство:
и.т.д.
Распространение формулы (7) для второго замечательного предела на любое значение аргумента. Способ стремления аргумента к бесконечности.
Доказательство: Для любого значения
Будем пользоваться свойствами степенной и показательной функции.
Примем теорему о сжатой переменной…ч.т.д.
Доказательство:
Формулы (11) и (12) записываются в виде однообразной формулы.
Объявление: |
|||
-
Телефоны +7-931-218-72-20
+7-921-572-15-04
Email:
zakaz@5forstudents.ru
Вконтакте:
-

-
-
-
Сайт работает
-
Расскажите о нас друзьям

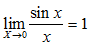
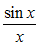
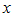
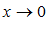
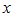
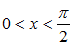
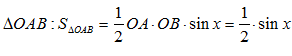
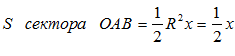
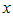
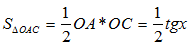
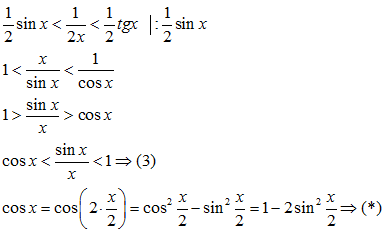
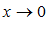
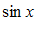 ,как меньшая величина, тоже стремиться к нулю. Из формулы (*) следует, что
,как меньшая величина, тоже стремиться к нулю. Из формулы (*) следует, что 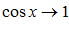 при
при 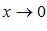 .По теореме о сжатой переменной и по формуле (3) заключаем, что
.По теореме о сжатой переменной и по формуле (3) заключаем, что 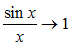 при
при 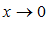 .
.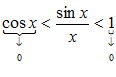
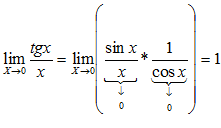
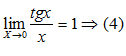
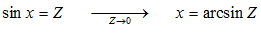
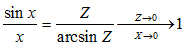
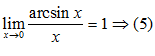
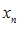
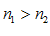
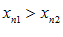
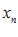 называется строго убывающей, если при
называется строго убывающей, если при 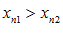 следует
следует 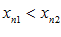 .
.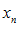 называется возрастающей в широком смысле, иначе не убывающей, если при
называется возрастающей в широком смысле, иначе не убывающей, если при 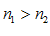 следует
следует 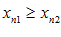 .
.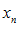 называется возрастающей в широком смысле, иначе не убывающей, если при
называется возрастающей в широком смысле, иначе не убывающей, если при 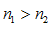 следует
следует 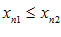 .
.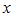 называются монотонными переменными. Они могут быть строго монотонными и не строго монотонными.
называются монотонными переменными. Они могут быть строго монотонными и не строго монотонными.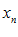
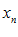
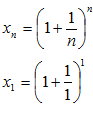
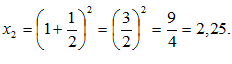
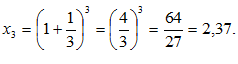
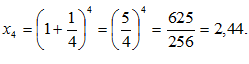
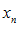 строго возрастает и ограничена сверху числом 3. По теореме о существовании предела и ограниченной монотонной переменной можно утверждать, что рассматриваемая переменная
строго возрастает и ограничена сверху числом 3. По теореме о существовании предела и ограниченной монотонной переменной можно утверждать, что рассматриваемая переменная 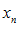 имеет предел:
имеет предел: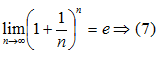
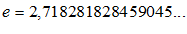
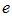 лежит в основании так называемых натуральных логарифмов.
лежит в основании так называемых натуральных логарифмов.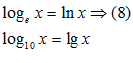
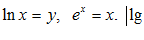
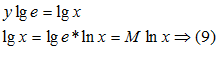
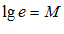 – модуль перехода.
– модуль перехода.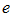 связано несколько функций, рассмотренных в математике.
связано несколько функций, рассмотренных в математике.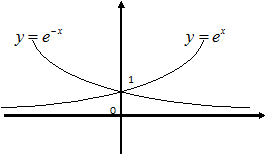
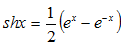 – синус гиперболический.
– синус гиперболический.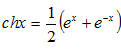 – косинус гиперболический.
– косинус гиперболический.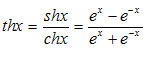 – тангенс гиперболический.
– тангенс гиперболический.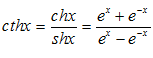 – котангенс гиперболический.
– котангенс гиперболический.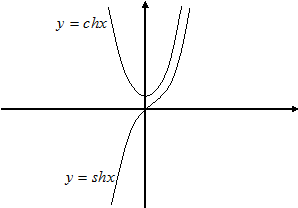
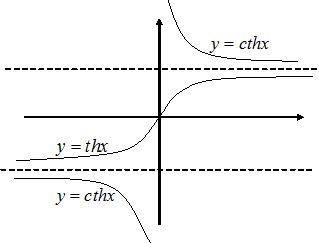
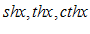
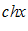
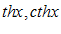
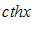
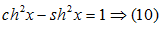
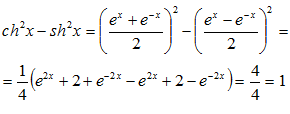
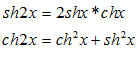
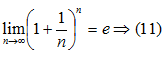
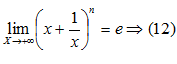
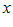 найдется такое натуральное
найдется такое натуральное 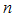 ,что будет выполняться неравенство:
,что будет выполняться неравенство: