Лекция №2: Определение функции.

Сначала разберемся с понятиям связка и квантор. К связкам относятся следующие символы:

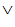— дизъюнкция

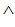— конъюнкция

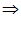— интликация     

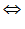— равносильность

    Этими символами связываются высказывания. Под высказываниями понимается предложения, относительно которых подразумевается, что оно ложное или истинное.

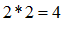    – истинно.

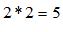    – ложно.

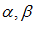– обозначение высказывания.

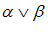– дизъюнкция двух высказываний.

Опр.1: Дизъюнкция истина тогда и только тогда, когда истинно хотя бы одно из данных высказываний.

Опр. 2:Логическим умножением (конъюнкция) называется высказывание, истинное тогда и только тогда, когда оба высказывания истинны.

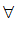– квантор всеобщности (любой, всякий, каждый).

 – существование (существует)

U– высказывание.

Ū – противоположное высказывание.

Определение функции

Опр. 1: Переменная величина y называется функцией аргумента x, если каждому рассматриваемому значению x из некоторого множества D соответствует определённое значение y из множества E.

D – область определения функции.

E– область значения функции.

Способы задания функции:

  • Аналитический способ. (Т. е. По формуле.)
  • Табличный.
  • Графический.
  • Программа (алгоритм).

Все способы могут использоваться совместно.

Классификация функций

  • Явные и неявные функции.

А)    Функция 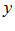называется неявной, если она задана уравнением 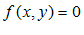, не решенным относительно .

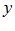Б)    Функция 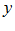называется явной, если она задана уравнением 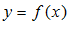решенным относительно .

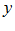  • Периодическая функция, если существует число T называемое периодом, обладает свойством:


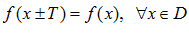
Функции делятся на АЛГЕБРАИЧЕСКИЕ и ТРАНСЦЕНДЕНТНЫЕ

Алгебраическая функция – когда она задана уравнением 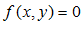 , где слева стоит многочлен с переменными x
 и y (неявная а. ф.).

Функция называется явной алгебраической, если для получения её значения над аргументом производится конечное число арифметических действия и действий извлекания корня натуральной степени.

ПРИМЕР:


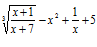
Все остальные функции относятся к трансцендентным – тригонометрические, обратные тригонометрические, логарифмические, показательные, степенные с иррациональным показателем.

Опр. 2: Функция называется четной, если при 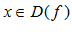, то на 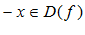и выполняется:

,.

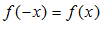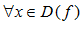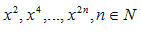
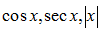
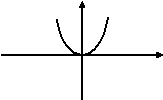График четной функции симметричен OY

 Опр. 3:Функция называется нечетной, если при 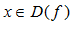, то на 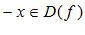и выполняется:

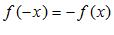
Например:

График нечётной функции симметричен относительно начала координат.

Опр. 4: Две точки называются симметричными относительно начала, если они лежат на одной прямой, проходящей через начало, по разные стороны от начала и на одинаковом расстоянии от начала.


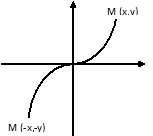
 Существуют такие функции которые не являются ни чётными ни нечётными.

Функции делятся на элементарные и неэлементарные.

 Основные элементарные функции:

 1.    Постоянная



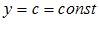
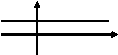
2.    Степенная:


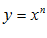
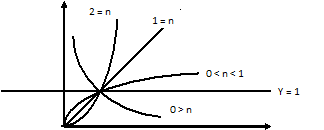
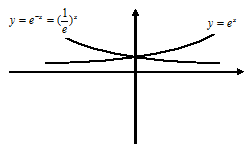
3. Показательная:

, , .


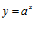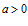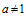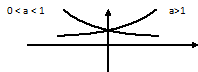
4.    Логарифмические:

, , .


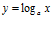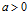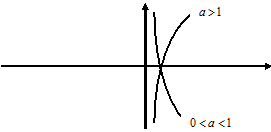
 5. Тригонометрические


 

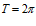
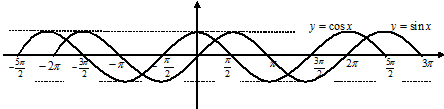
6. Обратные тригонометрические.

y = arccos x,y = arcctg x,y = arcsin x,y = arcctg x.


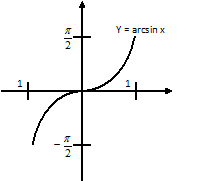
Определение сложной функции.

y = f(x)

X – область определения функции.

Y – область значения функции.

Z = j(y)    – отображаются в области Z.


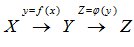
Z = j[f (x)]    – сложная функция, иначе композиция.

Сложная функция состоит из цепочки двух простых.

 Опр. 5: Элементарной функцией называется функция, состоящая из основных элементарных функций с помощью какого-либо числа арифметических операций и конечного числа образующих операций функции от функции.

Кроме того, требуется, чтобы эта функция была задана одним аналитическим выражением.

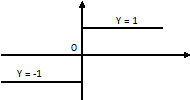
Неэлементарные функции – операции интегрирования, операции решения дифференциального уравнения, операции суммирования с бесконечным числом слагаемых и операции обратной функции с помощью нескольких аналитических изображений.


y(x)=sign(x)

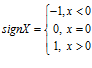
Объявление: