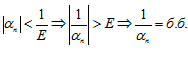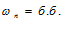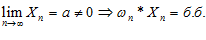Лекция №5. Бесконечно большие величины.
Опр. 1: Переменная
Неравенство (1) равносильно объединению 2-х неравенств:
По-другому:
Опр. 2: Объединения 2-х промежутков Бесконечно большие величины при своём изменении начиная с некоторого номера Пример:
1)
2) -2, 4, -8, 16, -32, …
Будем различать положительные и отрицательные бесконечно большие величины ЛЕММЫ О БЕСКОНЕЧНО БОЛЬШИХ. ЛЕММА №1: Величина обратная бесконечно малой есть бесконечно большая величина, и обратно… Доказательство: Пусть Это значит, что для любого сколь угодно большого числа
ЛЕММА №2: Произведение бесконечно большой величины на переменную, стремящуюся к конечному пределу отличного от нуля, есть бесконечно большая величина. |
|||
-
Телефоны +7-931-218-72-20
+7-921-572-15-04
Email:
zakaz@5forstudents.ru
Вконтакте:
-

-
-
-
Сайт работает
-
Расскажите о нас друзьям

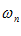 , называется бесконечно большой, если для любого, сколь угодно большого, числа
, называется бесконечно большой, если для любого, сколь угодно большого, числа 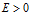 существует такой номер
существует такой номер 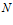 , что если
, что если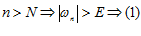
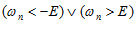 (где
(где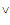 – «или»)
– «или»)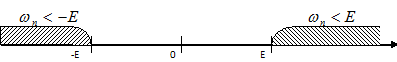
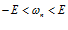

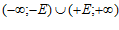
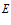
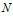 попадает в
попадает в 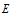 окрестность бесконечности и там далее остаётся.
окрестность бесконечности и там далее остаётся.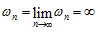 , если
, если 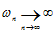
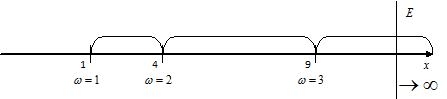
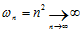
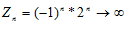
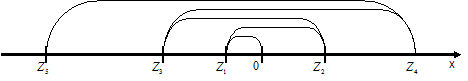

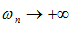 – положительные б.б.
– положительные б.б.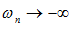 – отрицательные б.б.
– отрицательные б.б.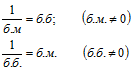
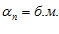 ,
, 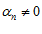
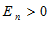 существует N такой, что при
существует N такой, что при 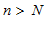 следует выполнение неравенства:
следует выполнение неравенства: