Лекция №7. Предел функции. Односторонние пределы

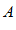Опр. 1: Постоянное число называется пределом функци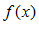и при 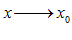, если для любого 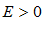существует число 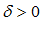, такое, что при выполнении неравенства 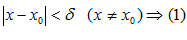следует выполнение неравенства .

    или    

Запишем неравенство (1) и (2) без модуля:

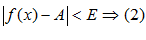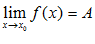
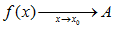
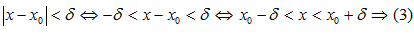
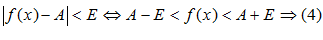
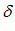Двойное неравенство (3) определяет – окрестность точки 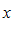на оси абсцисс.

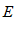Двойное неравенство (4) определяет – окрестность точки 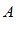на оси ординат.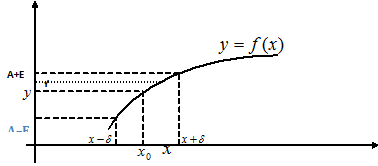

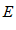Определение предела функции означает, что по выделенной производной

– окрестности точки 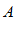на оси 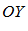определяется 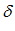– окрестность. Есть точка 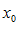на оси такая, что как только переменная 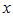попадает в 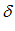– окрестность своей предельной точки 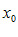, так сейчас же переменная 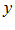попадает в 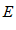– окрестность своего предельного значения .

Замечание

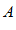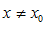В определении предела указывается, что т. к. в точке 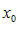функция может быть не определена.

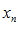Все теоремы о пределах, сформулированные и доказанные для случая переменной , т. е. последовательности, переносятся без существенных изменений на случай предела функции.

Односторонние пределы слева и справа .

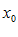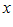Сформулированное определение предела в предыдущей лекции относится к так называемому двустороннему пределу, что означает, что переменная приближается к своему предельному значению с любой стороны, и слева, и справа. В некоторых случаях двусторонний предел может не существовать, но существуют односторонние пределы, когда переменная 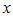приближается к 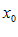только с одной стороны, или слева, или справа. В этом случае указывается соотношение 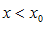или .

Запись

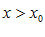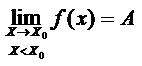     – предел слева.

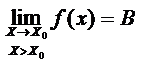     – предел справа

Второй вариант записи:

     – предел слева.

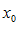ТЕОРЕМА: Для того, чтобы в точке существовал двусторонний предел функции, необходимо и достаточно, чтобы существовали оба односторонних предела и они были равны между собой:

Объявление: