Лекция №1 :МНОЖЕСТВА.

Опр. 1: Суммой множеств (объединением) – называют множество, каждый элемент которого принадлежит хотя бы одному из данных множеств.

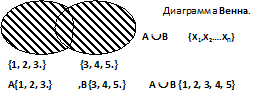
 Общий элемент указывается один раз.

Опр. 2: Пересечением множеств (произведением) называется множество, каждый элемент которого принадлежит данным множествам.

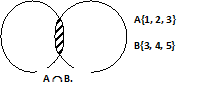
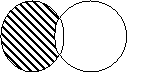
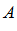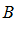Опр. 3: Разностью множеств и называют 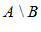множество, каждый элемент которого принадлежит 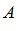и не принадлежит .

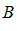Промежутки.

Вся ось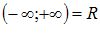 – множество вещественных чисел.

  

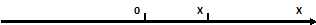
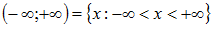
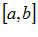– замкнутый промежуток – сегмент.

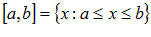
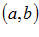– открытый промежуток (интервал).

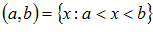
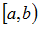– полузамкнутый.

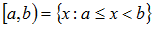
 РАЗЛИЧНЫЕ МНОЖЕСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ.

 1. Первичное множество

    N = {1, 2, 3….} – (применяются для счета предметов) множество натуральных чисел.

2.    {0, 1, 2, 3, 4…} – множество целых неотрицательных чисел.

3.    Z = {0, ±1, ±2…} – множество целых чисел.

4.    Q = {p/q} – рациональное множество чисел, где P Î Z, q = N.

Во множестве Q возможны все 4 арифметических действия, за исключением деления на нуль.

Множество иррациональных чисел – множество чисел, которые изображаются бесконечными не периодичными десятичными дробями.

Множество вещественных чисел (действительных) – множество, являющееся объединением Q и иррациональных чисел.

R – множество вещественных чисел.

R = Q È {иррациональные числа}.

Свойства вещественных чисел:

1. Упорядоченность.

Для любых двух вещественных чисел верно одно и только одно соотношение:

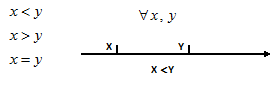2. Плотность:

Между двумя любыми не равными вещественными числами лежит бесконечное множество других вещественных чисел.

3. Неограниченность:

Каким бы не было вещественное число 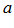, всегда существует точка 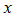, что 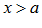, и всегда существует 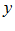, что

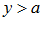
4. Несчетность.

Вещественные числа нельзя занумеровать, т. к. их больше натуральных (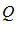 поддается нумерации.)

5. Непрерывность.

Опр. 1: Множество 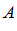называется ограниченным с верху, если существует его верхняя граница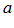
(число, которое не меньше всех чисел множества А)

 Если существует верхняя граница хоть одна, то существует бесчисленное множество верхних границ.

Опр. 2: Наименьшей из верхних границ, ограничивающих с верху числовое множество 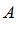, называется его точной верхней границей.

Обозначается: 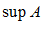(supremum)

Опр. 3: Множество 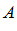называется ограниченным снизу, если существует его нижняя граница в (число, которое не больше всех чисел множества ).

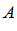 Если существует хотя бы одна нижняя граница, то существует бесчисленное множество нижних границ.

Опр. 4: Наибольшая из нижних границ, ограниченного снизу числового множества 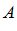, называют точной нижней границей.

Обозначается: 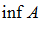(infimum).

Опр. 5: Множество называется ограниченным, если оно ограничено и сверху и снизу.

Формулировка свойства непрерывности множества вещественных чисел.

Если числовое множество 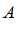ограниченно сверху, то оно имеет точную верхнюю границу.
Если числовое множество 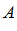  ограниченно снизу, то оно имеет точную нижнюю границу.

 

Читать далее: