Под числовой последовательностью х1, х2, х3, …, хn, … понимается функция xn=f (n), заданная на множестве натуральных чисел.

 Пример. Если известен общий член последовательности xn=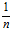, то соответствующая последовательность будет: 1, , , , …, , …

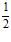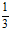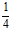Действия над последовательностями

Пусть {xn} и {yn} произвольные последовательности, содержащих одинаковое количество элементов.

Суммой (разностью) последовательностей {xn} и {yn}, называется последовательность, каждый член которой есть сумма (разность) соответствующих членов последовательностей {xn} и {yn}.


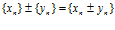
Аналогично определяются произведение и частное последовательностей {xn} и {yn}, в случае частного .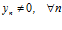

Частным случаем операции умножения последовательностей (если одна из последовательностей постоянна) является операция умножения последовательности на число: для того, чтобы умножить последовательность {xn} на число k, необходимо каждый член этой последовательности умножить на k, т.е.


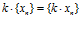
▼ Последовательность 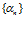называется бесконечно малой, если для любого сколь угодно малого положительного числа 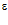можно подобрать такой номер N, что, начиная с этого номера (т.е. для всех 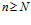), будет выполнено неравенство


▼ Последовательность {уn} называется положительной бесконечно большой, если для любого сколь угодно большого числа М найдётся такой номер N, что для всех n, начиная с этого номера, выполняется неравенство

|yn|>M

 Пример. уn=( –1)n – 1n, принимает значения: 1; –2; 3; –4; … Данная последовательность есть бесконечно большая величина, так как она становится и остаётся с некоторого номера N по абсолютной величине больше сколь угодно большого числа |M|, |yn|>M при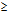 nN.

 ▼ Число а называется пределом последовательности {xn}, если для любого положительного числа 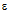можно подобрать такой номер N (как правило, зависящий от 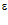), что, начиная с этого номера (т.е. для всех 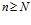). Будет выполнено неравенство


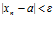
Операции над пределами последовательностей

1. Предел суммы (разности) двух сходящихся последовательностей равен сумме (разности) их пределов:

,

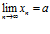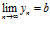
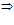
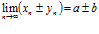
2. Предел произведения двух сходящихся последовательностей равен произведению их пределов:

,

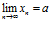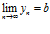
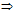
В частности:

  • постоянный множитель можно выносить за знак предела:

    ,

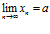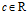
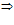
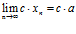
  • предел натуральной степени от сходящейся последовательности равен этой степени от её предела:

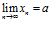
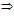
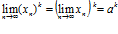    , k=1, 2, 3, …

  •  предел корня k-й степени от сходящейся последовательности равен корню этой же степени от предела последовательности:

  

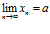
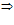
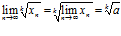
Постановка задачи. Пользуясь определением последовательности, доказать, что .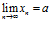

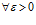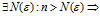
План решения. 1. Число а называется пределом последовательности {xn}, если для , 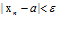. Это означает, что 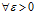неравенство 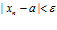имеет решение для .

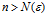2. Найти, при каких n справедливо неравенство 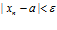, т.е. решить это неравенство относительно n.

3. Если решение имеет вид 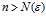, то а — предел числовой последовательности {xn}.

⋙Если решение неравенства 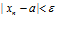нельзя представить в виде 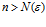, то число а не является пределом последовательности {xn}.

Пример 1. Пользуясь определением предела последовательности, доказать, что.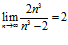

► 1. По определению число а =2 называется пределом числовой последовательности 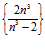, если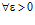
.

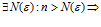
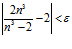2. Найдём, при каких n справедливо неравенство 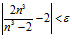, т.е. решим это неравенство относительно n.

3. Неравенство имеет решение 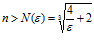. Следовательно, 2 — предел числовой последовательности .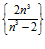