Лекция №3. Последовательность, предел последовательности

Опр. 1: Последовательностью называется множество чисел, пронумерованных с помощью чисел и расположенных в порядке возрастания номеров.

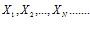
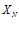– общий член последовательности.

    

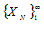
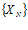
N – номер члена последовательности, играет роль аргумента функции. Фактически задает последовательность целочисленных аргументов.

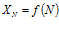– функция целочисленных аргументов.

Выражение примеров последовательности:

1. 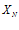    – общий член последовательности.

;

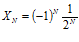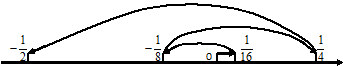
2.    

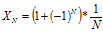
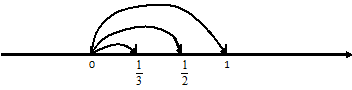
Будем различать последовательности, имеющие предел, и не имеющие предела. Общий член последовательности 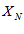– переменная величина, значение которого определяется номером N. Эта величина является функцией аргумента N

ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ.

Опр. 1: Постоянное число 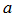 называется пределом переменной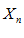, если для любого сколь угодно малого числа 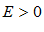, существует такой номер 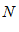, что при выполнении неравенства 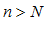следует выполнение неравенства:

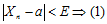
В силу леммы о вещественных числах (№1) одно неравенство с модулем (1) равносильно двойному неравенству:

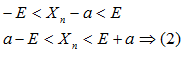
Неравенство (2) определяет на оси E так называемую E – окрестность точки a.

Неравенство (2) означает, что переменная точка 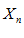 находится в E – окрестности точки a.

Постоянное число a называется пределом переменной 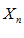, если для любой сколь угодно малой E – окрестности точки a начиная с некоторого номера n (n > N), точка 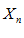попадает в эту E – окрестность, и при своем дальнейшем изменении будет там находиться.

 

 

 

 

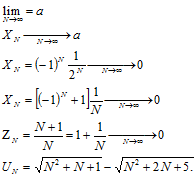
Объявление: